Session 03¶

Brief introduction about numpy and installation¶

Numpy is a library for the Python programming language, supports large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays.

Using Numpy in Python allow the user to write fast programs as long as most operations work on arrays or matrices instead of scalars.

We install Numpy library directly to our Python IDE.

Open a PyCharm, go to Settings-->Project(name_of_your_project)-->Project Interpreter. There you should add required packages by pressing + symbol and install numpy from available packages respectively.

If you once installed pandas library, then numpy library has already been installed automatically.

Basic steps¶

At first, let us implement simple examples of building vectors, matrix and list of numbers using arrays. Create a new python script file and write down:

#!/usr/bin/ python
import numpy as np

row_vec = np.array([1,2,3,6])
# creates a row (zeile) vector

col_vec = np.array([[7,8,9,12]]).T
# T stays for transpose and creates a column (spalte) vector

mat_vec = np.array([[1,2,3], [4,5,6], [7,8,9]])
# creates a matrix

ran = np.arange(10)
# range starts from 0 till 9

lin = np.linspace(0,2,4)
# creates an array with four equally spaced elements, starting with 0 and ending with 2


print("row vector is equal to: \n",row_vec)
print("column vector is equal to: \n",col_vec)
print("matrix vector is equal to: \n",mat_vec)
print("range is equal to: \n",ran)
print("linspace vector is equal to: \n",lin)

We get:

row vector is equal to:
[1 2 3 6]

column vector is equal to:
[[ 7]
 [ 8]
 [ 9]
 [12]]

matrix vector is equal to:
 [[1 2 3]
  [4 5 6]
  [7 8 9]]

linspace vector is equal to:
[0.         0.66666667 1.33333333 2.        ]

We can implement basic operations using scalar and arrays, like addition, subtraction, multiplication, division and exponentiation:

import numpy as np
lst = [2, 3, 7.9, 3.3, 6.9, -6, 0.11, 10]

v = np.array(lst)

We can not easily take a list of numbers and implement basic operations using scalar number. We should define first the list of numbers as an numpy array and implement basic operations. Otherwise, it will give a type error.

Task

Create a variable with a scalar number. Use all five basic mathematical operations using the scalar number and the list. Print the answers and check them.

When you are done with your python script, please push it to your personal git repository.

List comprehensions¶

List comprehensions is a very important part of Python. It provides a concise way to create lists. It consists of brackets containing an expression followed by a for clause, then if clauses.

The list comprehensions always returns a result list.

Let us see some examples regarding the list comprehensions.

We are given random list of numbers in old_list. We want to create a new_list containing the elements of old_list which are less than 50. Create a new python script and write down:

old_list = [88, 13, 28, 51, 19, 63, 92, 27]
new_list = []
for i in old_list:
    if i<50:
        new_list.append(i)

print(new_list)

We get:

[13, 28, 19, 27]

If we use here list comprehensions, we can get a concise form of list:

new_list = [i for i in old_list if i<50]
print(new_list)

We get the same result!

The list comprehensions starts always with square brackets [], reminding you that the result is going to be a list.

The basic syntax is:

[ do something **for** item in list **if** conditional ]

This is equivalent to:

for item in list:
  if conditional:
    do something

There are some more examples help you to understand it better.

We have to print range of numbers between 0 and 9 using list comprehensions. Create a new python file and write down:

x = [i for i in range(10)]
print(x)

#this will give the output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

In this example, we are initialising x with seven values and y as an empty list. What we want to do is to fill y with the values of x divided by 5.

The most boring way is:

x = [5, 10, 15, 20, 25, 30, 35]
y = []

for counter in x:
    y.append(counter / 5)

print("x = {} \ny = {}" .format(x, y))

Format function in Python has its own syntax. Curly braces {} define placeholders, whereas .format(value) returns a formatted string with the value passed as parameter in the placeholder position. In other words the values to be printed go inside {}, the actual values go inside .format().

We print the values and get:

x = [5, 10, 15, 20, 25, 30, 35]
y = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0]

Using list comprehensions, we obtain lighter version of commands:

z = [n/5 for n in x]
print("x = {} \nz = {}" .format(x,z))

We get:

x = [5, 10, 15, 20, 25, 30, 35]
z = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0]

If we compare it with the previous example, we see that we have replaced three lines with one line.

When you are done with your python script, please push it to your personal git repository.

Difference between list comprehensions and numpy¶

Why we can not just divide x by 5 directly? Let us try it. Create a new python file and write down:

#! /usr/bin/python
import numpy as np

x = [5, 10, 15, 20, 25, 30, 35]
a = x/5
print (a)

We will get:

TypeError: unsupported operand type(s) for /: 'list' and 'int'

This means, you can not anyway divide regular Python list by integer.

Or it is better to use here try-except block. It tries to run your code and if it finds an exception, it runs the except block.

In certain example, you can not divide list by 5, so it run the except block:

try:
   a = x / 5
except:
   print("you can not divide regular Python list by integer")

We get:

you can not divide regular Python list by integer

However, as we already mentioned before, we are able to solve this problem by using numpy arrays. We convert our x array to a numpy array with np.array command:

a = np.array(x)
b = a / 5

print("with numpy: a = {} \nb = {}".format(a, b))

We get:

with numpy: a = [ 5 10 15 20 25 30 35]
b = [1. 2. 3. 4. 5. 6. 7.]

Numpy arrays are effective when you deal with such operations. But, we need list comprehensions in many cases as well. We have seen with you both ways, so you can choose the best one for yourself.

When you are done with your python script, please push it to your personal git repository.

Plotting sin and cos waves¶

In this example, we are going to plot a few simple sin and cos graphs, getting an introduction to Python’s plotting library, Matplotlib. Create a new python file and write down:

#! /usr/bin/python

import numpy as np
import matplotlib.pyplot as plt

Matplotlib is a huge library. We are using only pyplot part of it.

We use linspace function. As we already implemented before, linspace generates evenly spread out values. We have to generate 1000 values between 0 and 8*pi. Pi number is approximately equal to 3.1415.

x = np.linspace(0, 8*np.pi, 1000)

It generates 1000 values which are floating point number by default.

Coming back to our code:

y1 = np.sin(x)
y2 = np.cos(x)

plt.plot(x, y1, "-g", label="sine")
plt.plot(x, y2, "-b", label="cos")
plt.ylim(-1.5, 1.5)

plt.legend(loc = "upper right")
plt.xlabel("x-axis: 0 to 8*pi")
plt.ylabel("y-axis: -1.5 to 1.5")

plt.show()

We are plotting the graph of sin function with green color (-g for green) and cos function with blue color (-b for blue). We are taking y1 as a function of x for the first graph and y2 as a function of x for the second graph.

We can also set the limits for the y-axis to be between -1.5 and 1.5. By default, it takes between -1.0 and 1.0.

Each function has its own label, sine and cos. We will show up them in the legend, at the upper right side of the graph. You can easily change the orientation of the legend, as you wish.

We can also manually change the labels of x-axis and y-axis, using .xlabel and .ylabel functions respectively.

We get:

Task

Why we are taking 1000 values for linspace instead 100? What do you think? Try with 100 and tell me the difference.

When you are done with your python script, please push it to your personal git repository.

Plotting salary vs names¶

In this exercise, we are going to read data from a file and plot it.

All .txt data under the scope of this course can be found in git repository: group Group Uno, project name Tutorial_IT2, folder name Praktikum 3. Copy these files directly to that folder, where you created your python file.

We have two files: names.txt and salaries.txt. The data in the two files are proportionally linked. So, Jack has a 0 salary, John has 100 and so on.

First we read salaries. Create a new python script and write down:

#! /usr/bin/python

import numpy as np
import matplotlib.pyplot as plt

salary = np.fromfile("salaries.txt", dtype=int, sep=",")
#        np.fromfile(file, dtype=float/int, sep="")

print(salary)

By using np.fromfile() command, we construct an array from data in a text or binary file.

One of the main features of numpy arrays, that makes them better than normal Python lists, is that it allows different types of number data types. Python lists are typically used for strings.

We set datatype dtype as int. This tells numpy that datatype is an integer.

The last element is sep=”,” function, which tells numpy that the data in the file is separated by commas. If the data in the array were seperated by colon, we would use sep=”:”.

We get:

0, 100, 200, 500, 1000, 1200, 1800, 1850, 5000, 10000

Now we read names:

names = np.loadtxt("names.txt",dtype='str',delimiter=",")
#       np.loadtxt(file, dtype=string/float,delimiter="")

print(names)

The np.fromfile() function does not work with text, so we are using loadtxt() function. It is similar to previous function.

We set datatype dtype as str. This tells numpy that datatype is a string.

The last element is delimiter=”,” function. It is the same as sep() function, but the latter function is not used to separate string values.

We get:

['Jack' 'John' 'Matt' 'James' 'Sarah' 'Jessica' 'Rupert' 'Pablo' 'Rolanda' 'Bill Gates']

Now we need to plot the names vs the salaries. We can not really plot the names on the x-axis, as the x-axis has to be a number.

However, we are able to manage it. The first thing we do is to create a variable x that will contain numbers for each of the names:

x = np.arange(len(names))

The numpy arange generates a list of numbers starting from 0. In our code, x contains a list of numbers from 0 up to the quantity of names.

plt.bar(x,salary)
plt.show()

! Once you got a graph, please make a comment to plt.show() in order not to get confused with later graphs.

We plot x vs salary. We are using a bar graph here. We get:

We should replace the numbers on the x-axis with actual human names. Because we can only plot against numbers, we had to use this approach.

plt.xticks(x, names)
plt.show()

! Once you got a graph, please make a comment to plt.show() in order not to get confused with later graphs.

If one need to replace names on the y-axis, one should write yticks(). However, in our case, we leave as it is. We get:

We set x and y labels here. Also we should add a title.

plt.xlabel("Names")
plt.ylabel("Salaries")
plt.title("Salary of 10 random people")
plt.show()

! Once you got a graph, please make a comment to plt.show() in order not to get confused with later graphs.

We get a final graph here:

Numpy also supports many functions like maximum, minimum and average values in the array.

max_np = np.max(salary)
min_np = np.min(salary)
aver_np = np.average(salary)

print(max_np, min_np, aver_np)

If we look at the graph above, we realise that the two first and two last values suppress every other values on the background.

Let us modify the graph, so that the graph will illustrate the salaries of people except for Rolanda and Bill Gates.

Before that, we should practice some features of Python. Create a new python file and write down:

a = np.arange(5)
print(a)

print(a[:3])

print(a[2:])

print(a[2:4])

print(a[:-1])

print(a[-1:])

Check the printed outputs and read the followings to understand how it is going on.

We create a list a that contains values from 0 up to 4 (the last element remains unread).

a[start value : end value]

Either start value or end value can be empty, in which case it will start at the beginning or go to the end. We can also give both values.

What does -1 mean? Since the list starts at zero, -1 is the last element. -2 is the second last element, and so on.

So, we will use this last trick to get rid of the two first and two last values in our data. We go back to previous python script, where we have been working with names and salary data:

salaries_new = salary[2:-2]
names_new = names[2:-2]

x = np.arange(len(names_new))
plt.bar(x, salaries_new)
plt.xticks(x, names_new)

! Before plotting the graph, make sure that you made a comment also to plt.bar(x, salary), because you already have a new plt.bar() function here:

plt.show()

We get:

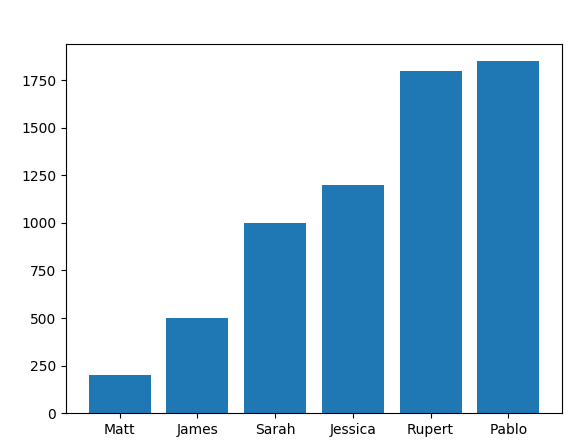
Task

Please, find the maximum, minimum and average values of a new data by yourself.

When you are done with your python script, please push it to your personal git repository.

At last, let us compare the time comparison between Python lists and Numpy arrays. One of the main advantages of numpy is its time advantage over standard python. In the following we define two functions:

Try to understand the code. If you have further questions regarding the code, please feel free to ask. Create a new python script and write down:

import numpy as np
import time as t

size_of_vec = 10000

def pure_python_version():
    t1 = t.time()
    X = range(size_of_vec)
    Y = range(size_of_vec)
    Z = [X[i] + Y[i] for i in range(len(X))]
    return t.time() - t1

def numpy_version():
    t1 = t.time()
    X = np.arange(size_of_vec)
    Y = np.arange(size_of_vec)
    Z = X + Y
    return t.time() - t1

t1 = pure_python_version()
t2 = numpy_version()

print(t1, t2)
print("NumPy is in this example " + str(t1/t2) + " faster!")

If the Run Window shows an error, check size_of_vec to 100000 or even to 1000000. The reason for the error is that in your computer numpy calculated 10000 elements almost in 0 second. Therefore the error was caused due to zero division.

Define with bigger numbers in what extent numpy array is faster than with python lists.